Flow Regimes in a Re-entry Trajectory

As an object moves through the air, the air molecules near the object are disturbed and move around the body. The reaction of air because of the object depends upon the ratio of the speed of the object with the speed of the sound. The information about the object travels as disturbances in the medium with the speed of sound. If any object is moving at a speed less than the speed of sound, the fluid molecules ahead of the object sense the disturbance created by the object and move around it. But if the object is moving at a speed more than the speed of sound, then the fluid near the disturbance cannot react or “get out of the way” before the disturbance arrives and a shock wave is formed before the object. Because of the importance of this speed ratio, aerodynamicists have designated it with a special parameter called the Mach number in honor of Ernst Mach, a late 19th century physicist who studied gas dynamics. Flow regimes are thus characterized based on Mach number.

Hypersonic flows $M_{\infty} > 5$
Supersonic flows $M_{\infty} > 1.2$ and $M_{\infty} < 5$
Transonic flows $0.8 > M_{\infty} > 1.2$
Subsonic flows $M_{\infty} < 0.3$

The hypersonic flow is encountered at the early stages of re-entry and ends with the subsonic flow at low altitudes after fragmentation of the object.

For Earth, atmospheric entry occurs at the Kármán line at an altitude of about 100 km above the surface (source: wiki) and the speeds of the objects entering the atmosphere are in the order of several $km/s$. For example, a space shuttle in orbit has a mass of 100 $ton$, an orbital velocity of 7700 $m/s$ , and an altitude of 300 $km$. It becomes obvious to assume that a very significant part of the re-entry of an object will be subjected to hypersonic flow. Also, it is important to note that, during the re-entry trajectory the object experiences flow regimes of different rarefaction. At the start of the re-entry, the flow is extremely rarefied and gradually the atmosphere becomes thicker and we reach continuum regime. The degree of rarefaction is quantified by Knudsen number (Kn), which is defined as the ratio of the mean free path $(\lambda)$ of the gas molecules to the characteristic length scale (L).

\[Kn = \frac{\lambda}{L}\]

A variety of non-intuitive physics in rarefied gas flows has been observed experimentally [1]. Depending on the value of Kn, the flow-field is generally divided into the following regimes [2]:

Continuum regime (Kn < 0.001)
Slip regime (0.001 < Kn < 0.1)
Transitional regime (0.1 < Kn < 10)
Free-molecular regime (Kn > 10) .

Some Important Physical Phenomena During Re-entry

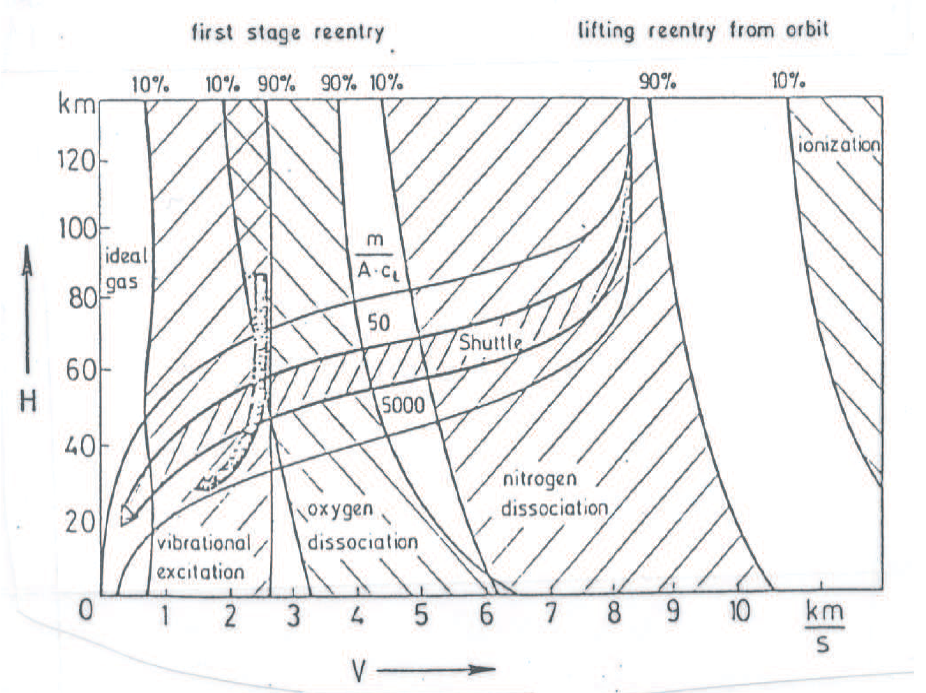
The behaviour of a perfect gas at large Mach numbers can be easily calculated and it has several distinctive features than for flows with Mach numbers below 5. In hypersonic flows, small changes in Mach number are associated with large changes of temperature rather than of flow pattern (than from $M_{\infty} < 5$). However, the approximation of a perfect gas becomes increasingly less valid with increase of speed mainly because of the associated high temperatures; molecular vibration, dissociation and even ionization effects become important [3]. Boundary layers on bodies thicken and threaten to fill the narrow regions of air flow aft of the leading edge shocks, and interaction effects curve these shocks and introduce large entropy gradients (see Fig.1). The subject is therefore a complex one, particularly when flight at very high altitudes and low densities is included for which the air can no longer be regarded as a continuum.

**Fig.1:** A shadow-graph image of a re-entry capsule in hypersonic flow.

This section discussed about the aspects of aerodynamics, gas-surface interactions, structural thermomechanical response, and object fragmentation.

Aerodynamics and aerothermodynamics

As noted in the above paragraphs, a space object goes through different flow regimes during a re-entry trajectory. The hypersonic regime is dominating from 120 km to 50 km altitude and breakups usually occur during the hypersonic flow phase. The breakup/fragmentation of a vehicle/object is due to the high-temperature and structural stress concentration due to aerothermodynamic load. In a very general sense, significant features of hypersonic flows are as follows,

Thin shock layer (see Fig.1)
Mach number independence [4]
Viscous boundary layer (see Fig.1)
Reactive flow field (See Fig.2)

( This section will be updated in more detail during the next update to the Stardust-R Wiki )

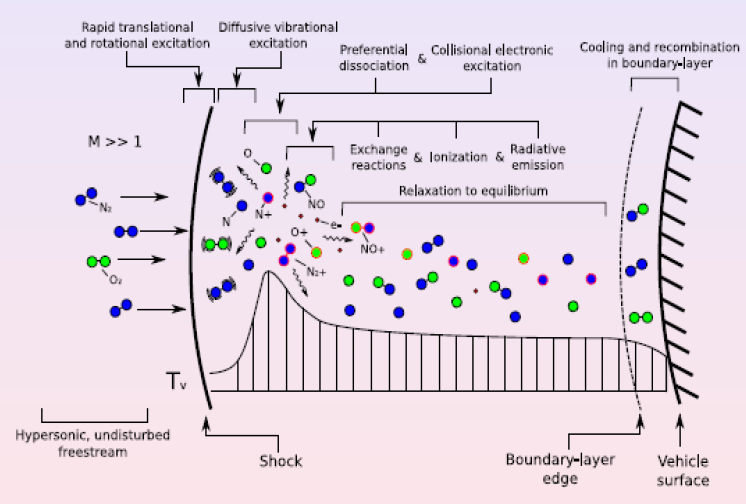
**Fig.2:** Velocity-altitude map showing various thermo-chemical reaction regimes.

Gas-surface interactions (GSI)

Gas-surface interactions (GSI) play a very fundamental role in the transfer of energy from the aerothermodynamic flow-field into the re-entry vehicle/object. Viscous dissipation in the boundary layer can lead to very high gas temperature, molecular dissociation, gas radiation (also shock-layer radiation), and wall radiation. As a result, the gas interacts with the object surface through molecular recombination, convective heat transfer, radiation, and ablation. All those interactions consist of exchanges of energy or mass. Hence, a proper estimation of GSI is very crucial to the sizing and accurate modeling of a thermal protection system(TPS) and the subsequent re-entry trajectory. The Fig.3 shows different chemical reactions that can happen during a hypervelocity entry. Accurate modeling of these chemical reactions is essential to predict the overall heat load during re-entry. Several on-going experimental campaigns are

( This section can be updated in more detail during the next update to the Stardust-R Wiki )

**Fig.2:** Various gas-surface reaction mechanisms.

Structural behavior during re-entry

Fragmentation analysis

References

[1] Narasimha, Roddam. Some flow problems in rarefied gas dynamics. Diss. California Institute of Technology, 1961.
[2] Schaaf, S. A., and P. L. Chambre. “Flow of Rarefied Gases, High Speed Aerodynamics and Jet Propulsion.” Fundamentals of Gas Dynamics. Vol. 3. Princeton University Press NY, 1958.
[3] Brun, Raymond, ed. High Temperature Phenomena in Shock Waves. Vol. 7. Springer Science & Business Media, 2012.
[4] Kliche, D., Ch Mundt, and E. H. Hirschel. “The hypersonic Mach number independence principle in the case of viscous flow.” Shock Waves 21.4 (2011): 307-314.